MATEMATINĖS LOGIKOS IR AIBIŲ TEORIJOS PRADMENYS. 1

3. Binariniai sąryšiai. 7

4. Kombinatorikos elementai 8

4 TEMA.. 11

GEOMETRINIAI ASPEKTAI 11

5. Padėtis erdvėje ir atstumas. 11

6. Linijų vaizdavimas. 15

7. Interpoliavimas ir ekstrapoliavimas. 18

8. Fraktalai: būdas vaizduoti natūraliems objektams. 19

5 TEMA.. 23

Topologijos elementai 23

9. Tinklai ir grafai 23

10. Grafų modeliai 25

11. Geografinės informacijos geometrija. 29

3 TEMA

MATEMATINĖS LOGIKOS IR AIBIŲ TEORIJOS PRADMENYS

1. Matematinė logika

Induktyvioji logika tiria samprotavimo dėsningumus, kurie priklauso ne nuo mąstymo turinio, o nuo jo formos. Logikos matematizavimo idėją pirmasis pasiūlė G.Leibnicas (1646-1716), kuris manė, kad visas turimas žiniais galima išskaidyti į paprasčiausius elementus, pažymėti juos specialiais simboliais, apibrėžti veiksmų su tais simboliais teisykles – ir bus galima lengvai gauti naujas išvadas, patikrinti ar teisingi samprotavimai. Taigi, iškilo poreikis įvesti simbolius sąvokoms ir ryšiams tarp jų žymėti. Leibnico idėja iš principo neįgyvendinama, bet jo mintis iš dalies realizavo Dž. Bulis (1815-1864) matematizuodamas logiką. Apžvelgsime elementarias jos sąvokas.

Teiginiai ir predikatai.

Pavyzdžiui, “48 dalijasi iš 6”, “Kur vakar buvai?”, “5<3”

Apibrėžimas. Teiginys – tai sakinys, kuris išreiškia tiesą arba netiesą.

Teiginys gali būti užrašytas raidėmis ar kitais simboliais, pvz., p,r,q. Teiginio teisingumo reikšmė yra funkcija T(p)

Jei teiginys p išreiškia tiesą, T(p)=1, kitaip T(p)=0. Matematinė logika ir tiria, kaip nustatyti sudėtingų teiginių teisingumo reikšmes.

Kaip matome, yra sakinių, kurie nėra teiginiai, pvz., klausiamasis sakinys.

Išnagrinėkime dar porą pavyzdžių:

x>0

a+b=b-a

(a+b)c=ac+bc

Negalima nustatyti šių teiginių teisingumo, nežinant kintamojo reikšmės – jie gali tapti ir klaidingais, ir teisingais.

Apibrėžimas. Predikatas – tai sakinys su kintamaisiais, kuris tampa teiginiu vietoje kintamųjų įrašius konkrečias jų reikšmes.

Predikatus žymėsime kaip jų kintamųjų funkcijas didžiosiomis raidėmis, pvz., P(a, b).

Loginės operacijos

Teiginiai skirstomi į paprastuosius ir sudėtinius. Paprastuoju laikomas eiginys, kurio negalima suskaidyti į kitus teiginius. Sudėtiniai teiginiai sudaromi iš kitų teiginių (paprastų ar sudėtinių) sujungiant juos loginėmis jungtimis. Išskiriamos penkios jungtys:

a) netiesa, kad;

b) arba;

c) ir;

d) tada ir tik tada, kai;

e) jeigu ..., tai.

Sudėtinių teiginių sudarymas naudojantis šiomis operacijomis – tai loginės operacijos.

1. Neigimas. Jei p – teiginys, tai teiginys “netiesa, kad p” (dažnai sakoma “ne p”) vadinamas teiginio p neiginiu ir žymimas ¬p; Jo teisingumo reikšmė T(¬p)=1-T(p).

2. Disjunkcija (loginė sudėtis). Jei p ir q – teiginiai, tai teiginys “p arba q” vadinamas teiginių p ir q disjunkcija arba logine suma ir žymimas p V q; Teiginių p ir q disjunkcija neteisinga vieninteliu atveju – kai p ir q abu neteisingi.

3. Konjunkcija (loginė daugyba). Jei p ir q – teiginiai, tai teiginys “p arba q” vadinamas teiginių p ir q konjunkcija arba logine sandauga ir žymimas p&q. Teiginių p ir q konjunkcija teisinga vieninteliu atveju – kai p ir q abu kartu yra teisingi.

4. Implikacija. Jei p ir q – teiginiai, tai teiginys “jeigu p, tai q” vadinamas teiginių p ir q implikacija ir žymimas p=>q. Implikacija p=>q yra neteisingas teiginys tada ir tik tada, kai p teisingas, o q – neteisingas. Tai įdomi savybė, praktiškai reiškianti, kad iš neteisingos prielaidos bet kokia išvada yra formaliai korektiška. Implikacija dar gali būti skaitoma: “iš p išplaukia q”; “p yra teiginio q pakankamoji sąlyga”; “q yra teiginio p būtinoji sąlyga”.

5. Ekvivalencija. Jei p ir q – teiginiai, tai teiginys “p tada ir tik tada, kai q” vadinamas teiginių p ir q ekvivalencija (tapatumu). Ekvivalencija žymima póq arba p º q. Ji teisinga, kai p ir q teisingumo reikšmės sutampa, o klaidinga – kai jos skiriasi. Dar skaitoma “p būtina ir pakankama, kad būtų q” arba “q būtina ir pakankama, kad būtų p”.

Pavyzdžiai

p – “metai turi 12 mėnesių”, q – “sniegas yra žalias”, r – “sniegas yra baltas”.

¬p, ¬q, ¬r - ?

T (p V q) =1; T(p V q V r) =1; T(p&r) = 1; T(q&r) = 0; T(p&q&r) = 0.

T(p=>q) = 0. T(q=>p) = 1. T (p º r) = 1;

Galima sudaryti elementarių loginių operacijų teisingumo reikšmių lenteles.

p	q	p V q	p&q	p=>q	p º q
0	0	0	0	1	1
0	1	1	0	1	0
1	0	1	0	0	0
1	1	1	1	1	1

Sudėtingesni teiginiai sudaromi taikant keletą loginių operacijų. Pavyzdžiui, (p=>q)&(q V r).

Loginės formos ir logikos algebra.

Apibrėžiant logines operacijas jungiamiems teiginiams nekeliami jokie reikalavimai, o domina tik teisingumo reikšmės. Taigi, teiginius galima žymėti tiesiog raidėmis. Pačios raidės, taip pat elementarios operacijos vadinamos pagrindinėmis loginėmis formomis. Jei juose vietoje raidžių įrašysime kokius nors kitus teiginius, paprastus ar sudėtinius, vėl gausime teiginius.

Apibrėžimas. Loginė forma – tai reiškinys, gautas baigtinį skaičių kartų panaudojus loginių operacijų ženklus ir skliaustus raidėms sujungti.

Pavyzdžiui, reiškiniai (p=>q) V ¬p&r), ((p=>q) V¬p&r))=>r.

Predikatų skaičiavimas taikomas įrodymuose, programavimo kalbose, duomenų bazių valdymo sistemose.

Dvi loginės formos, kurių teisingumo reikšmių lentelės sutampa, vadinamos logiškai ekvivalenčiomis.

Loginė forma, kurios teisingumo reikšmė yra 1 nepriklausomai nuo ją sudarančių teiginių teisingumo reikšmių, vadinama tautologija ir žymima I.

Loginė forma, kurios teisingumo reikšmė yra 0 nepriklausomai nuo ją sudarančių teiginių teisingumo reikšmių, vadinama tapačiai klaidinga (loginiu nuliu) ir žymima O. Akivaizdu, kad ¬I º O, ¬O º I.

Matome, kad loginės formos panašios į algebros reiškinius (sudėtis, daugyba, nulis, vienetas, lygybė).

Aptarsime paprasčiausias loginių operacijų savybes.

Dvigubo neigimo dėsnis.

¬¬p º p

Tai pagrindinė neigimo savybė. Teisingumu įsitikiname iš lentelės.

Disjunkcijos savybės

1) p Vp º p (disjunkcijos idempotencijos dėsnis);

2) p V ¬p º I (negalimo trečiojo dėsnis);

3) p V I º I

4) p Vq º q Vp (komutatyvumo dėsnis);

5) (p Vq) Vr º p Vq Vr) (asociatyvumo dėsnis)

6) p V O º p.

Konjunkcijos savybės

1) p &p º p (konjunkcijos idempotencijos dėsnis);

2) p & ¬p º O (prieštaravimo dėsnis);

3) p & I º p

4) p & q º q & p (komutatyvumo dėsnis);

5) (p &q) &r º p &q &r) (asociatyvumo dėsnis)

6) p & O º O.

Kai kurios implikacijos savybės

(p=>q) º ¬p Vq

(p º q) º (( p=>q)&  (p=>q ))

Logikos dėsniai

Kiekviena tautologija vadinama logikos dėsniu. Kai kurie dėsniai buvo minėti nagrinėjant loginių operacijų savybes.

Kontrapozicijos dėsnis.

(p=>q) º( ¬q=> ¬p)

Silogizmo dėsnis.

[((p =>p1)& (p1 => q)) => (p =>q)] ºI

De Morgano dėsniai.

¬ (p Vq) º ¬p & ¬q

¬ (p &q) º ¬p V ¬q

Prieštaros (suvedimo į prieštaravimą) dėsnis

(p & ¬q) => (r & ¬r) º(p =>q)

Teisingos išvados taisyklė (modus ponens)

Jei teiginiai p ir p=>q – teisingi, tai ir q teisingas.

Neteisingos išvados taisyklė (modus tollens)

Jei teiginys p=>q yra teisingas, o q – neteisingas, tai ir p – neteisingas.

Visus dėsnius galima įrodyti remiantis jų teisingumo reikšmių lentelėmis.

2. Aibių algebra

Aibę galima nusakyti išvardijant jos elementus arba nusakant jos elementų požymį. Pavyzdžiui B = {b₁, b₂, b₃}; A = {x| x Î Z, x<100}; N = {a| a₁ = 0, a_i+1 = a_i+3}

Aibė yra viena iš pagrindinių matematikos sąvokų. Kaip sąvoka visumos elementų, turinčių juos jungiantį požymį, ji atsiranda praktiškai kiekvienoje teorijoje, nors žodis “aibė” ir nevartojamas. Todėl svarbu mokėti iš turimų aibių konstruoti naujas aibes, t.y., mokėti aibių veiksmus ir pagrindines jų savybes.

Sakinį “a priklauso aibei A” užrašysime: a ÎA. Jei a nėra aibės A elementas, rašysime aÏA. Aibę vadinsime baigtine, jei jos elementų skaičius baigtinis ir begaline, jei jos elementų yra be galo daug, pvz., N, Z, C. Skaiti aibė – tokia, kurios elementus įmanoma iš eilės sunumeruoti (Z, Q, bet ne R).

Jei aibė apibrėžta ne išvardijant elementus, o kokia nors taisykle, gali būti taip, kad ji neturės nė vieno elemento. Tokią (apibrėžtą) aibę vadinsime tuščiaja aibe ir žymėsime Ø . Pavyzdžiui, aibė dirbančių gyventojų, priklausančių amžiaus grupei 0-10.

Jei kiekvienas aibės A elementas yra ir aibės B elementas, sakoma, kad A yra B poaibis, o B – aibės A viršaibis. Tai žymima A <B arba B >A. Pavyzdžiui, {a, b, c} <{a, b, c, d}.

Remiantis poaibio apibrėžimu, kiekviena aibė yra savo pačios poaibis. Tuščiąją aibę galima laikyti betkurios kitos aibės poaibiu. A <A; Ø  <A. Šie du aibės A poaibiai vadinami netiesioginiais, o kiti (jei jų yra) – tiesioginiais. Nesunku įsitikinti, kad sąryšis “poaibis” turi tokią savybę:

(A <B) & (B <C) => (A <C).

Laikysime, kad visi vienos aibės elementai yra skirtingi. Jei dvi aibės A ir B turi tuos pačius elementus (tuo atveju jos yra viena kitos poaibiai), jas vadinsime lygiomis ir rašysime A=B.

Nagrinėdami konkretų tam tikros teorijos klausimą, niekada nesusiduriame su visomis galimomis aibėmis, o tik su tomis, kurios tiesiogiai siejasi su sprendžiamu uždaviniu. Patogu apibrėžti universaliąją aibę I, kuri būtų visų toje teorijoje nagrinėjamų aibių viršaibis. Tada bet kuri tos visumos aibė A yra I poaibis. Pavyzdžiui, įvairios amžiaus grupės, dirbančiųjų tam tikrose ūkio šakose, moterų, alkoholikų, imigrantų aibės yra Gyventojų universaliosios aibės poaibiai.

Aibių sudėtis.

Apibrėžimas. Aibių A ir B suma arba junginiu vadinama aibė, sudaryta iš visų elementų, priklausančių bent vienai iš duotųjų aibių. A ir B suma žymima AÈB arba A+B.

Bendrieji sudedamų aibių elementai įeina į sumą tik vieną kartą (pagal susitarimą, kad aibės elementai yra skirtingi). Pavyzdžiui, {1,2,3}È{1,3,4,7}={1,2,3,4,7}; “mergaitės” U ”berniukai”=”vaikai”. Aibių sudėtis atitinka teiginių disjunkciją:

A +B = {a| a ÎA Va ÎB } arba

a Î A U B º a ÎA V a Î B

Toks formalus apibrėžimas patogus, kai aibės apibrėžtos požymiais. Pavyzdžiui, kai A = {x| P(x)} ir B = {x| Q(x)}, A UB = {x| P(x) VQ(x)}.

Aibių sudėties savybės.

1. Jeigu A <B, tai A UB = B.

2. A UB = B UA (komutatyvumas)

3. (A UB) UC = A U (B UC)(asociatyvumas)

4. A U A = A

5. A U Ø = A

6. A U I = I

Pirmosios 3 savybės akivaizdžios; sekančios 3 yra pirmosios savybės išvados. Daugumą savybių galima praplėsti bet kokiam skaičiui aibių.

Aibių daugyba.

Apibrėžimas. Aibių A ir B sankirta arba sandauga vadinama aibė, sudaryta iš visų elementų, priklausančių abiems iš duotųjų aibių. A ir B sankirta žymima A ∩ B arba AB.

Pavyzdžiui, {1,2,3} ∩ {1,3,5,7} ={1,3}; “moterys” ∩”vaikai”=”mergaitės”; “moterys” ∩ ”berniukai”= Ø. Aibių daugyba atitinka teiginių konjunkciją:

A ∩B = {a| a ÎA &a Î B } arba

a Î A ∩B º a ÎA & a ÎB

Pavyzdžiui, kai A = {x| P(x)} ir B = {x| Q(x)}, A ∩B = {x| P(x) &Q(x)}.

Aibių daugybos savybės.

1. Jeigu A <B, tai A ∩B = A.

2. A ∩B = B ∩A (komutatyvumas)

3. (A ∩B) ∩C = A ∩ (B ∩C)(asociatyvumas)

4. (A UB) ∩C = (A ∩C) U (B ∩C) (daugybos distributyvumas sudėties atžvilgiu)

5. A ∩A = A

6. A ∩ Ø = Ø

7. A ∩ I = A

Kaip ir sudėties atveju, daugumą savybių galima praplėsti bet kokiam skaičiui aibių.

Aibių atimtis.

Apibrėžimas. Aibių A ir B skirtumu vadinama aibė tų aibės A elementų, kurie nepriklauso aibei B. A ir B skirtumas žymimas A\B.

Pavyzdžiui,{1,2,3,4,7}\{1,2,3}={4,7};“vaikai”\”vyrai”=”mergaitės”; “moterys”\”berniukai”=“moterys”.

A \ B = {a| (a ÎA) & (a ÏB) } arba

a Î A \B º (a ÎA) & (a ÏB) 

Pavyzdžiui, kai A = {x| P(x)} ir B = {x| Q(x)}, A\B = {x| P(x) & ¬Q(x)}.

Skirtumas I\A vadinamas aibės A papildiniu ir žymimas A* .

A* = {a| a ÏA}

Aibių skirtumo savybės.

1. A\B = A ∩B*

2. Jeigu A Ì B, tai A\B = Ø

3. A\ Ø = A

4. Jeigu A ∩B = Ø , tai A\B = A

5. (A\B) ∩C = (A ∩ C) \(B ∩ C)

6. (A\B) ÈB = A È B

Aibių papildinio savybės.

1. A ÈA* = I

2. A ÈA* = Ø

3. I* = Ø

4. Ø * = I

5. A** = A

Oilerio ir Veno diagramos

Dažnai patogu aibes vaizduoti grafiškai. Paveiksle parodytos figūros, reiškiančios aibių operacijų rezultatus.

Remiantis diagramomis, lengvai galima patikrinti dvi lygybes, vadinamas de Morgano dėsniais (jie visiškai analogiški logikos de Morgano dėsniams):

1. (A ∩B)* = A* ÈB*

2. (A È B)* = A* ∩B*

Kvantoriai.

Iš predikato P(x) teiginį gausime tik įrašę vietoje x kokią nors konkrečią reikšmę. Pavyzdžiui, “Vidutinės gyventojų grupės pajamos yra 1000 Lt/mėn”, jei I = Gyventojai, bus teisingas, jei gyventojai = “gyventojai su aukštuoju išsilavinimu”.

Teiginius iš predikatų galima sudaryti ir naudojant kvantorius.

Sakinys “(aibėje A) egzistuoja toks elementas, kuriam P(x) – teisingas teiginys” sutrumpintai rašomas: ($x Î A): P(x); $x: P(x) – jei A universali. Pavyzdžiui, “egzistuoja gyventojas, kurio pajamos lygios 1000 Lt/mėn.” Ženklas $ vadinamas egzistavimo kvantoriumi. (angl.: exists).

Sakinys “Visiems x (iš aibės A)” teiginys P(x) yra teisingas sutrumpintai užrašomas ("x Î A): P(x); "x: P(x) – jei A universali. Ženklas " vadinamas visuotinumo kvantoriumi. (angl.: all). Pavyzdžiui, “Kiekvieno gyventojo (x) su aukštuoju išsilavinimu (A) pajamos ne mažesnės 1000 Lt/mėn.”

Teiginiai, sudaryti su kvantoriais, jungiami pagal tas pačias taisykles, kaip ir paprasti teiginiai. Pavyzdžiui, ¬("x Î A): P(x); ("x Î A): ¬P(x); ¬($x Î A): P(x); ($x Î A): ¬P(x).

“Egzistuoja gyventojas (x) su aukštuoju išsilavinimu (A), kurio pajamos yra mažesnės kaip 1000 Lt/mėn.” º“Netiesa, kad kiekvieno gyventojo (x) su aukštuoju išsilavinimu (A) pajamos ne mažesnės 1000 Lt/mėn.”

Labai svarbu tiksliai suformuluoti teiginius ir atskirti, kurie iš jų yra logiškai ekvivalentūs, o kurie – ne.

Aibių Dekarto daugyba.

Vienodiems objektams atskirti paprastai vartojame numerius, pvz., telefono abonentų. Tačiau kartais vieno numerio nepakanka objektui žymėti ir tenka jam priskirti 2 skaičius ar kokių kitokių ženklų porą. Porų sudarymas atitinka aibių Dekarto daugybos operaciją.

Apibrėžimas. Aibių A ir B Dekarto sandauga (kombinatorine sandauga) vadinama aibė porų (a,b), kuriuose a yra bet kuris aibės A elementas, o b – bet kuris B elementas. Žymima A x B

Pavyzdžiui, {1,2} x {3,4} = {(1,3),(2,3),(1,4),(2,4)}. A x A (Dekarto kvadratas).

Dekarto daugyba nėra nei komutatyvi, nei asociatyvi, bet pasižymi distributyvumu aibių sąjungos ir sankirtos atžvilgiu.

Dekarto daugybą galima praplėsti bet kokiam skaičiui aibių: A₁ x A₂ x... x A_n. Nesunku pastebėti, kad jei visos aibės A_i yra baigtinės ir kiekviena turi po m_i elementų, tai Dekarto sandaugoje A₁ x A₂ x... x A_n yra m₁m₂m₃...m_n elementų. Jei bent viena aibė begalinė – sandauga taip pat begalinė, pavyzdžiui, jei A = {1} o B = R, tai geometriškai sandaugą galima pavaizduoti kaip tiesę, lygiagrečią y ašiai einančią per tašką (1,0).

3. Binariniai sąryšiai.

Sąryšis (ryšys, priklausomybė) gali sieti du ar daugiau tos pačios arba skirtingų aibių elementų. Sąryšis tarp 2 elementų vadinamas binariniu. Tai tam tikras požymis, jungiantis tuos elementus. Pavyzdžiui, santuoka yra binarinis sąryšis tarp vyrų ir moterų aibių. Galimas sąryšis toje pačioje aibėje. Tiksliai neapibrėžtą, dar tik intuityviai suvokiamą sąryšį aibėje arba tarp dviejų aibių Dekarto sandaugos pagalba galima nagrinėti kaip konkretų matematinį objektą.

Apibrėžimas. Sąryšis f Ì A x B tarp aibių A ir B elementų vadinamas funkcija (funkciniu sąryšiu) jei ((x, y₁) Î f & (x, y₂) Îf) => (y₁ = y₂)

Praktiškai tai reiškia, kad kiekvieną x iš aibės A atitinka vienintelis y iš B. Šis apibrėžimas gal ir ne visai įprastas, bet labai konkretus: funkcija – tai tam tikru būdu sudaryta aibė.

Apibrėžimai.

Sąryšis f Ì A x A vadinamas refleksyviu, jei kiekvienas A elementas a tuo sąryšiu yra susietas pats su savimi.

("a ÎA) (a, a) Îf

Sąryšis f Ì A x A vadinamas simetriniu, jei kiekvieną aibės A elementų porą (a,b) atitinka pora (b, a) ,susieta tuo pačiu sąryšiu.

"(a, b) Îf : (b, a) Îf

Sąryšis f Ì A x A vadinamas tranzityviu, jei elementams a ir b bei b ir c esant susietiems tuo sąryšiu, juo susieti ir elementai a ir c.

"(a, b) Îf, (b, c) Î f: (a, c) Îf

Pavyzdžiui, santuoka žmonių aibėje yra simetrinis, bet ne refleksyvus sąryšis. Ar jis yra tranzityvus? Sąryšis “vyresnis už” toje pačioje aibėje yra tranzityvus, bet ne simetrinis ir ne refleksyvus. Sąryšis “gyvena viename mieste” turi visas 3 savybes.

Apibrėžimas.

Sąryšis f Ì A x A, kuris yra refleksyvus, simetrinis ir tranzityvus, vadinamas ekvivalentumo sąryšiu.

Taigi, jei modelyje mus domina tik žmogaus gyvenamoji vieta, du skirtingus asmenis, gyvenančius viename mieste, matematiniu požiūriu galima laikyti “vienodais”.

Visuma aibės A elementų, susietų ekvivalentumo sąryšiu su jos elementu a, vadinama ekvivalentumo klase ir žymima K_a.

Teorema. Bet kurios ekvivalentumo klasės arba sutampa, arba neturi bendrų elementų.

Įrodymas. Tegu aibėje A apibrėžtas ekvivalentumo sąryšis f. Tarkime, kad egzistuoja K_a. ir K_b, turinčios bendrą elementą c. Tegu a ir b – bet kurie elementai atitinkamai iš K_a. ir K_b. Iš komutatyvumo reikalavimo: (a, c) Î f ir (c, b) Î f; tada iš tranzityvumo savybės: (a, b) Î f. Taigi, a Î K_bir b Î K_a. Tai reiškia, kad K_a< K_b ir K_b< K_a. Vadinasi, K_a= K_b.

Aibė, kurioje apibrėžtas ekvivalentumo sąryšis, suskirstoma į nesikertančias ekvivalentumo klases. Taigi, apibrėžus kokią nors aibės skirstymo sąlygą, užtenka patikrinti 3 paprastas savybes ir žinosime, ar prasminga pagal ją klasifikuoti.

Apibrėžimai.

Sąryšis f Ì A x A turi trichotomijos savybę, jei su kiekviena aibės A elementų pora (a,b) teisingas vienas ir tik vienas iš šių teiginių:

1) (a,b) Î f;

2) (b,a) Î f;

3) a = b

Sąryšis f Ì A x A vadinamas tiesinės tvarkos sąryšiu, jei jis yra tranzityvus ir turi trichotomijos savybę.

Aibė, kurioje apibrėžtas tiesinės tvarkos sąryšis, vadinama sutvarkyta aibe. Tokio sąryšio pavyzdys naudojamas GIS – “yra dešinėje”. Pagal jį visus objektus geografiniame sluoksnyje galima sutvarkyti taip, kad jie seks vienas po kito tolygiai keičiantis požymiui.

Binarinius sąryšius ir jų savybes galima apibendrinti keleto aibių Dekarto sandaugai.

4. Kombinatorikos elementai

Nustatėmę, kad tiesiškai sutvarkyti aibę reiškia išdėstyti jos elementus tam tikra tvarka. Keliais skirtingais būdais galima sutvarkyti baigtinės aibės elementus? Intuityviai aišku, tik kad tokių būdų skaičius yra baigtinis.

Jungdami, perstatydami, tvarkydami aibės elementus, gauname elementų rinkinius, kuriuos vadiname aibės elementų junginiais (kombinacijomis). Pavyzdžiui, iš aibės {a,b,c,d} elementų galime sudaryti rinkinius {a,b,c}, {c,b,a}, {c,c,c,c} ir kt. Matematikos šaka, nagrinėjanti junginių sudarymo dėsningumus ir junginių skaičius, vadinama kombinatorika.

Tegu aibėje A yra n skirtingų elementų. Juos naudosime junginiams sudaryti. Visus junginius galima skirstyti į paprastus (arba tiesiog junginius, kurių visi elementai skirtingi (jie yra A poaibiai) ir kartotinius, kuriuose gali būti sutampančių elementų (jie nėra A poaibiai). Junginius galima sudaryti ir iš skirtingų aibių.

Kombinatorinė daugybos taisyklė.

Jei elementą a₁ galima parinkti iš aibės A₁, turinčios m₁ elementų, elementą a₂ galima parinkti iš aibės A₂, turinčios m₂ elementų ir t.t. iki n, tai rinkinį (a₁, a₂, ... a_n) galima sudaryti m₁m₂...m_n skirtingų būdų.

Gretiniai, kėliniai, deriniai

Apibrėžimas. Gretiniu iš n elementų po k vadinamas bet kuris sutvarkytas n elementų aibės poaibis, turintis k elementų (k-naris gretinys).

Du gretiniai laikomi skirtingais, jei jie skiriasi bent vienu elementu arba jų eilės tvarka. Pavyzdžiui, iš 3 elementų aibės {a,b,c} galima sudaryti šešis 2 elementų gretinius ab, ac, bc, ba, ca, cb. Pirmajam elementui yra 3 pasirinkimai, antrajam lieka vienu mažiau ir t.t.

Derinių skaičius iš n po k žymimas A^k (pranc.: arrangement) ir lygus n(n-1)(n-2)... (n-k+1), kas lygu n!/(n-k)!

Apibrėžimas. Kėliniu iš n elementų vadinamas gretinys iš n po n

Pavyzdžiui, iš 3 elementų aibės {a,b,c} galima sudaryti 6 kėlinius abc, acb, bac, bca, cab, cba.

Galimų kėlinių iš n elementų skaičius žymimas P_n (pranc.: permutation) ir lygus n! Tai skirtingų n elementų aibės sutvarkymo būdų skaičius.

Apibrėžimas. Deriniu iš n elementų po k vadinamas bet kuris n elementų aibės poaibis, turintis k elementų

Pavyzdžiui, iš 3 elementų aibės {a,b,c} galima sudaryti tris 2 elementų derinius ab, ac, bc.

Derinio atveju nenurodyta elementų tvarka, taigi deriniai gali skirtis tik savo elementais. Galimų derinių iš n elementų skaičius žymimas C^k (pranc.: combinaison) ir lygus n!/k!(n-k)! t.y., A^k/ k!

Kartotiniai junginiai

Gretiniai, kuriuose elementai gali kartotis, vadinami kartotiniais gretiniais. Kartotinių gretinių iš n elementų po k skaičius yra n^k. Pavyzdžiui, iš 3 elementų aibės {a,b,c} galima sudaryti devynis 2 elementų gretinius ab, ac, bc, ba, ca, cb, aa, bb, cc. T. y., yra 3 būdai parinkti pirmąjį elementą, kiekvienam iš jų - 3 būdai parinkti antrąjį ir t.t. 3² šiuo atveju.

Kartotiniai gretiniai, kuriuose elementai kartojasi jiems nurodytą skaičių kartų, vadinami kartotiniais kėliniais. Tegu kiekvienas aibės A elementas a₁ .. a_k gali kartotis a_i kartų. Pavyzdžiui, iš 3 skaitmenų 1, 1 ir 2 galima sudaryti tris kartotinius gretinius 112, 121, 211. Galimas kartotinių gretinių skaičius yra (atmetami vienodi kurių yra po n_i!)

P(n₁, n₂, .. n_k) = n!/n₁!n₂! ... n_k!

Kartotiniai deriniai iš n elementų po k yra vienodi, jei juos sudaro tie patys elementai, paimti po tiek pat kartų (tvarka nesvarbi). Jų gali būti

(n+k-1)!/k!(n-1)! . Pavyzdžiui, iš 2 elementų aibės {a,b} galima sudaryti keturis 3 elementų kartotinius derinius aaa, bbb, abb, baa.

4 TEMA

GEOMETRINIAI ASPEKTAI

5. Padėtis erdvėje ir atstumas

Geometriniai aspektai yra ypač svarbūs dirbant su geografine informacija: tai taškai, linijos, paviršiai, kūnai, erdvės-laiko objektai.

Pagrindiniai klausimai, į kuriuos reikia atsakyti, tai:

· Objektų padėties nustatymas

· Informacijos vaizdavimas

· Erdvinės savybės ir ryšiai

· Transformacijos

Padėtis. Daugelyje pažinimo sričių labai svarbu nustatyti skirtingų objektų padėtį. Matematikai yra sukūrę daug sistemų ir priemonių aprašyti objektams erdvėje. Aprašomoji geometrija užsiima matavimais (kampų, atstumų ir kt.). topologinė geometrija tiria formas. Fraktalų geometrija tiria matavimų skaičių, struktūros reguliarumą ir fragmentaciją – ji taikoma tiriant neapibrėžtus, netolydžius objektus. Objekto padėtis koordinačių sistemoje gali būti nusakyta įvairiai.

· 2, 3, ar daugiau matavimų (padėtis plokštumoje, erdvėje ar erdvėje-laike) ir kitos geometrinės nuorodų sistemos savybės (Dekarto, polinė ir kt.)

· Tolydžios ar diskrečios nuorodos

· Izotropinės ar anizotropinės sąlygos

· Formos ir atstumų kitimas laike ir keičiant mastelį

· Kokybinių ir kiekybinių savybių erdvėje matavimas

· Objektų kontūrai: aiškūs ar neapibrėžti; kintantys.

Tai yra, kalbant apie padėtį, reikia atsižvelgti į erdvės geometrines savybes, metriką ir paties objekto prigimtį.

Dažniausiai padėtis nusakoma dvimatės ar trimatės erdvės srityse koordinačių poromis ar tripletais.

A(x₁, y₁)

O(x₀, y₀)

A (ρ,φ) ir A (x₁, y₁)

ρ = √((x_1- x₀)²+(y_1- y₀)²)

φ = arcsin (y/ ρ) = arccos (x/ ρ)

arba x = ρ cos φ; y = ρ sin φ.

Dekarto ir polinės koordinatės naudojamos skirtingais atvejais, pavyzdžiui, kraštovaizdžio architektui, planuojančiam parko teritoriją, nereikia žinoti geografinės ilgumos ir platumos, bet ji būtina kalbant apie globalią geoinformacinę sistemą. Atskaitos taško parinkimas taip pat gali tapti problema. Dažniausiai koordinačių ašys yra statmenos, t.y., laikomos tarpusavyje nepriklausomomis. Tačiau gali būti situacijų, kai pasirenkamos pasvirusios ašys, parodant jų tarpusavio sąryšį, pavyzdžiui, naudojant kai kuriuos statistinius metodus.

Diskrečių objektų padėtis gali būti nurodyta adresu, aprašymu (topologinė charakteristika) arba apimančiu bloku.

Atstumas. Ilgio matmuo ypač svarbus. Matavimo metrika – tai atstumas tarp objektų erdvėje.

Metrika – tai reali funkcija ρ, apibrėžta aibėje X ir kiekvienai porai (x,y) iš X priskirianti skaičių ρ(x,y), vadinamą atstumu. Metrika turi tenkinti sąlygas:

1. ρ(x,y) >= 0; ρ(x,y) = 0 tada ir tik tada, kai x=y

2. ρ(x,y) = ρ(y,x)

3. ρ(x,z) <= ρ(x,y) + ρ(y,z)

Jei funkcija netenkina 2 sąlygos, ji vadinama kvazimetrika. Pavyzdžiui, jei gatvė yra vienos krypties. Jei funkcija gali įgyti neigiamas reikšmes, ji vadinama pseudometrika.

Kiekvienoje aibėje galima apibrėžti diskrečią metriką : ρ(x,y) = 1, jei x nelygu y ir 0, jei x=y.

Viena aibė gali turėti kelias skirtingas metrikas, pavyzdžiui, Euklido plokštumoje:

x = (x1,x2); y = (y1,y2);

ρ1(x,y) = ; ρ2(x,y) = max (|x1-y1|, |x2-y2|); ρ2(x,y) = |x1-y1|+|x2-y2|;

Atstumai priklauso nuo erdvės geometrijos tipo. Jos nereguliarumas iškreipia atstumų matavimus. Pasiekiamumas – pagal savo prigimtį yra daugialypė sąvoka. Atstumai, išmatuoti žemėlapiuose, ar gauti kokiu nors kitu būdu, gali būti didesni arba mažesni, negu realūs. Kartais svarbiausias yra temporalinis atstumas.Nors vertindami atstumą dažniausiai remiamės Euklido geometrija, kitos geometrijos gali pasirodyti labiau tinkamos. Kartais apskritai geriau atstumą įvertinti ne pagal koordinates, o topologiškai.

1. Plokštumoje Dekarto koordinačių sistemoje, kai erdvė tolydi, atstumai skaičiuojami naudojant koordinačių porų duomenis (1. pav., a).

2. Manheteno atstumas (b) – ne trumpiausia linija, o taškus jungiančiomis gatvėmis. Taip išmatuotas atstumas visada būna ne mažesnis už tiesioginį. Jis gali būti matuojamas virš paviršiaus arba realiais judėjimo keliais.

3. Atstumas erdvės tinkle. Pasirenkant tolydaus lauko modelį, dažniausiai neįvertinamos realios kliūtys ir judėjimo kanalai. Galima laikyti, kad judėjimas galimas tik tinkle, ne visoje plokštumoje. Neatitikimas tarp tiesinio ir realaus atstumo tinkle tuo didesnis, kuo netaisyklingesnis ar retasnis yra tinklas. Be to, galima įvertinti ne tik fizinį atstumą tinkle, bet ir judėjimo skirtingomis atkarpomis kainą (c).

4. Neplanarinis atstumas. Norint dar tiksliau nustatyti fizinį atstumą, reikia žinoti reljefo aukščio gradientus ir į juos atsižvelgti (d). be abejo, atstumai ant trimačio paviršiaus ne mažesni už planarinius. Atstumai gali būti įvertinti klaidingai, jei naudojamos netinkamos projekcijos, pavyzdžiui, stačiakampė projekcija, labai iškraipanti tikruosius atstumus ir dydžius – tokių dabar atsisakoma (e).

5. Žmonės keliones žemės paviršiumi dažnai vertina pagal sąnaudas – kainą arba sugaištą laiką. Transporto planuotojai, miestų geografai ir kt. kuria metodus erdvinei varžai matuoti. O kartografai turi metodus pavaizduoti santykines padėtis skirtingose metrikose, nors tai ne visada yra lengva.

6. Kai erdvė tolydi, atstumus galima vertinti pagal įvairiu būdu išskirtas artimumo zonas, dažniausiai apibrėžiamas azimutinėse sistemose (f). Jos, pavyzdžiui, sukuriamos prekybos centrams, taip parodant santykines jų pasiekimo sąnaudas. Perdengiant zonas, lengva palyginti atstumus: pavyzdžiui, nuo A iki C atstumas yra 6, nuo A iki B – tik 5.

7. Akumuliaciniai atstumai – nuo vieno taško iki daugelio kitų taškų – naudojami pasiekiamumo žemėlapiams sudaryti (g). Atstumai skaičiuojami statistiškai, įvertinant skirtingus kelius, skirtingu laiku, ir išvedant vidurkį.

8. Anizotropinėmis sąlygomis reguliarias struktūras iškreipia barjerai (įveikiami arba ne, h). Jei barjeras yra neįveikiamas (siena, valstybės siena) – atstumas gali virsti begaliniu. Įveikiami barjerai didina laiko sąnaudas/kainą arba mažina pralaidumą. Atstumai skaičiuojami atskirai kiekvienam segmentui su skirtinga erdvės varža ir sudedami.

Anizotropinėmis sąlygomis skaičiuojant atstumus reikia atsižvelgti į daug faktorių. Pavyzdžiui, didėjant skrydžio nuotoliui, kelionės lėktuvu kaina kinta logaritmiškai – mažėja kiekvienam 1000 km. Dažnai pavaisduoti tokiems atstumams naudojami kintantys masteliai.

Dar sudėtingesnė yra situacija, kai reikia įvertinti atstumus nuo keleto taškų. Tam naudojami specialūs kartografavimo metodai, pavyzdžiui, izolinijų aibės. Jos naudojamos ir kognityviniams žemėlapiams sudaryti. Matematiškai galima įrodyti, kad kai kurių atstumų neįmanoma parodyti žemėlapyje – tenka naudoti diadų matricas.

6. Linijų vaizdavimas

Kalbant apie geografinius objektus, dažniausiai kyla du klausimai:

1. Kaip generalizuoti?

2. Kaip vaizduoti?

Paveiksle (a) parodyti galimi kreivių vaizdavimo būdai. Generalizavimas – tai sudėtingo kontūro aproksimavimas panašiu su mažesniu skaičiumi būdingų taškų.

Kartografijoje naudojami metodai, kurie eliminuoja taškus sistemingai iš visų turimų digituotų ar kitaip įrašytų duomenų. Idealiu atveju turi išlikti visi pagrindiniai formos elementai ir topologinės savybės. Paveiksle (b) matyti, kaip generalizuojant upės liniją pasikeičia topologija: viena gyvenvietė nebe ant upės, kita – nebe prie upės. Vadinasi, kai kurie taškai (pavyzdžiui, objektų sąlyčio ir sankirtos) turi išlikti savo vietose bet kuriuo atveju. Tokie taškai vadinami topologiniais mazgais, tarp kurių galimos formos variacijos, pagal tai, kiek ta forma svarbi (pavyzdžiui, generalizuojant Lietuvos kontūrą paliekama Kuršių nerija).

Paprasčiausia generalizavimo procedūra – išmesti kas kelintą tašką. Tačiau ji visai negarantuoja, kad bus išsaugota forma.

Yra daug kitokių procedūrų, orientuotų į formos išlaikymą. Panagrinėsime dvi iš jų.

1. Kampų ir atstumų cenzas.

Išmetami taškai, kurie yra arba per arti kaimynų, arba per mažu kampu nukrypę nuo jų (c). Užduodamas minimalus leistinas atstumas ir kampas. Tada 3 taškus apimantis langelis slenka linija ir jame taikoma ši procedūra: antrajam taškui įvertinamas atstumas nuo prieš tai buvusio ir kampas, sudaromas atkarpų 1-2 ir 2-3. Jei vienas iš šių dydžių (arba abu ) yra per mažas, antrasis taškas išmetamas.

2. Linijos galai sujungiami tiesia linija ir matuojami visų taškų atstumai statmeniu iki tos linijos (d).

Jei atstumai yra mažesni už nurodytą tolerancijos atstumą, atitinkami taškai išmetami. Tolimiausias taškas imamas kaip nauja viršūnė ir procedūra kartojama abiems linijos dalims.

Galima kreivės atkarpas koduoti ir kryptimis, paskui išmetant pasikartojančias (e). Kuo daugiau numatyta krypčių, tuo tikslesnė aproksimacija. Bet apskritai, operuojant kodais generalizuoti yra sunkiau.

Aproksimavimas. Splainai

Tuo pačiu tikslu – sumažinti informacijos kiekį – linijos gali būti vaizduojamos kreivėmis. Splainas – tai kreivė, priderinama prie digituotos laužtės, kuri prieš tai dar gali būti generalizuota (pav., f). Kreivė gali kirsti arba liesti linijos segmentus. Saugoma kreivės lygtis tarp charakteringų taškų, o tarpiniai taškai gaunami iš lygties. Taip laužtė aproksimuojama kreive.

Idealiu atveju aproksimuojanti kreivė turi tenkinti šias savybes:

1. Ji turi eiti per visus charakteringus taškus.

2. Kreivės liestine 1 taške gali būti tik vienas aproksimuojamos laužtės segmentas arba kreivė kerta vienintelį segmentą.

3. Kreivė turi būti tolydi, glodi ir gražiai išreiškiama matematiškai.

Splainas – tai dizainerių naudojamas lekalas. Jis pagal kreivumo spindulius priderinamas prie būdingų kontūro taškų.

Matematiškai tai yra funkcija y = f(x); Čia f dažniausiai yra polinominė funkcija, t.y., f(x) =Σ a_ixⁱ, i kinta nuo 0 iki n.

Kubinis splainas (n = 3) dažniausiai naudojamas ir geriausiai tinka 4 iš eilės einantiems taškams aproksimuoti. Jis lengvai apskaičiuojamas ir gali atitinkti pakankamai sudėtingą kontūrą (g). Polinomo koeficientai išskaičiuojami įvairiais metodais, dažniausiai statistiniais. Polinominės funkcijos gali būti naudojamos ne tik kreivėms, bet ir paviršiams modeliuoti.

Pavyzdys. Paprasčiausias aproksimavimo metodas.

Turime keturis taškus Dekarto stačiakampėje koordinačių sistemoje: A(-2,1), B(0,0), C(1,1), D(2,3).

Aproksimuosime laužtę kubiniu polinomu y = ax³+bx²+cx+d.

Pareikalausime, kad jis eitų per visus tris duotus taškus ir sudarysime 4 lygčių sistemą.

-8a+4b-2c = 1; a+b+c = 1; 8a+4b+2c = 3; d = 0. Ats.: a = d = 0, b = c = 1/2, y = 1/2x²+1/2x.

Ir ištirkime funkciją: minimumo, maksimumo taškai, vingio taškai, išgaubtumas.

Pavyzdys. Dar kartą paprasčiausias aproksimavimo metodas.

Turime 4 taškus Dekarto stačiakampėje koordinačių sistemoje: A(-2,1), B(0,0), C(2,2), D(3,1).

Aproksimuosime laužtę kubiniu polinomu y = ax³+bx²+cx+d.

Pareikalausime, kad jis eitų per visus tris duotus taškus ir sudarysime 4 lygčių sistemą.

Ats.: a = -1/24, b = 3/8, c = -5/16, d = 0.

Ir ištirkime funkciją: minimumo, maksimumo taškai, vingio taškai, išgaubtumas.

Pagrindinė aproksimavimo polinomais problema yra ta, kad kiekvieną x gali atitikti tik viena y koordinatė, todėl kai kurių kreivių pavaizduoti neįmanoma. Mažiausiai, gali prireikti papildomų procedūrų, pavyzdžiui, pasukti koordinačių ašis ar kitaip transformuoti.

Dar patogesnė yra parametrinė išraiška, kai vietoje vienos lygties kreivei aprašyti sudaromos dvi lygtys, naudojant parametrą t.

Pavyzdys. Parametrinė atkarpos lygtis

Turime du taškus Dekarto stačiakampėje koordinačių sistemoje: A(x₁, y₁), B(x₂, y₂).

x = tx₂+(1-t)x₁

y = ty₂+(1-t)y₁; t iš intervalo [0,1]

Tokiu būdu perbėgami visi atkarpos taškai.

Sudėtingiau, kai reikia parametrine forma aprašyti kreivės lanką, pavyzdžiui, apskritimo.

x = Rcosα +x₀

y =Rsinα +y₀

R = R√ (x₀- x₁)²+(y₀- y₁)²

Ne kiekviena kreivė turi paprastą algoritmą jai generuoti. Bet yra kreivių šeima (Bezjė kreivės, sukurtos Reno automobilių kompanijai, Hermito ir kt.), kurių bendra išraiška:

x(t) = at³+bt²+ct+d.

y(t) = et³+ft²+gt+h.

jei kreivė trimatė, dar reikia atsižvelgti į z koordinatę:

z(t) = pt³+qt²+rt+s ; t iš intervalo [0,1]

Čia, kaip ir funkcinėje išraiškoje, geriausia pusiausvyra tarp skaičiavimų sudėtingumo ir aproksimacijos tikslumo pasiekiama kubiniais polinomais:

x(t) = A(t)x₁+ B(t)x₂+ C(t)x₃+ D(t)x₄ir t.t.

A(t)… S(t) – specialios kubinių polinomų funkcijos.

Kreivės gali būti skirtingos, priklausomai nuo skirtingų galinių ir vidinių taškų įtakos ir kitų reikalavimų (pav, a). Svarbi kreivės glodumo sąvoka – tai yra, kiek kartų ji tolydžiai diferencijuojama. Kreivės glodumo reikalavimas išreiškiamas išvestinių lygybe sandūros taškuose.

Viena lygtis ir kelių taškų koordinatės pakeičia ilgas digituotų koordinačių sekas. Tarpiniai taškai apskaičiuojami.Toks informacijos saugojimo metodas vadinamas intensyviu. Jis labai tikslingas kranto linijoms, upėms, mažiau – geležinkeliams, administracinėms riboms.

7. Interpoliavimas ir ekstrapoliavimas

Tai dydžio nežinomų reikšmių nustatymas remiantis žinomomis. Dažnai turime nepakankamai informacijos, tarkim keletą reljefo aukščio taškų, geologinių gręžinių, duomenų apie gyventojus ir pan. Jei reikia informacijos apie kokį nors parametrą nežinomuose taškuose, tenka “atspėti” (pav, b).

Paprasčiausiu atveju turim 2 taškus (x_0, y₀) ir ( x_1, y₁).

Bet kuris taškas tarp jų:

y = (x-x₀)( y₁-y₀)/(x₁-x₀)

Tiesė, einanti per taškus (1,1) ir (3,2): y = (x+1)/2

Interpoliaciniai polinomai.

Tarkime, kad keletui taškų (x_i, y_i) žinomos n kartų tolygiai diferencijuojamos funkcijos reikšmės y(x_i), i = 0, 1…n.

Reikia rasti y(x), kai x nesutampa nė su vienu x_i.

Sudaromas interpoliacinis polinomas, kurio reikšmės taškuose x_i sutampa su funkcijos reikšmėmis y_i, i = 0, 1…n.

Lagranžo formulė:

P_n(x) = * y_k

Pavyzdys. Pritaikysime Lagranžo formulę 3 taškams:

Turime 3 taškus Dekarto stačiakampėje koordinačių sistemoje: A(1, 3), B(2,1), C(4,2).

n = 2.

Ats. P₂(x) = (11x²-57x+64)/6. Ištirsime kreivę.

Polinomai nėra vienintelis būdas rasti funkcijos reikšmei nežinomuose taškuose. Tarkime, kad turimi duomenys – taškai plokštumoje, o nežinoma informacija – funkcijos reikšmė tuose taškuose. Tai – paprasčiausias atvejis. Interpoliavimu vadinsime procesą, kurio metu randamos funkcijos reikšmės tarpiniuose taškuose; ekstrapoliavimu – kai randamos funkcijos reikšmės taškuose, esančiuose už turimos imties ribų. Abiems procesams naudojami panašūs metodai.

Metodai (pav, c):

1. Artimiausios reikšmės. Nežinoma reikšmė prilyginama funkcijos reikšmei artimiausiame iš žinomų taškų.

2. Vidutinės reikšmės. Nežinoma reikšmė prilyginama vidutinei funkcijos reikšmei žinomuose taškuose.

3. Tiesinės interpoliacijos. Nežinoma reikšmė randama ant atkarpos, jungiančios funkcijos reikšmes taškuose iš kairės ir iš dešinės arba per 2 artimiausius žinomus taškus.

4. Interpoliacijos splainais. Nežinoma reikšmė randama ant kreivės, einančios per funkcijos reikšmes gretimuose taškuose.

5. Tikimybinės (stochastinės) interpoliacijos. Tarp kiekvienų 2 ar daugiau žinomų taškų generuojamos vidurkinės reikšmės su atsitiktiniu nuokrypiu. Tai metodas, susijęs su fraktalų parametrais.

6. Interpoliavimas pagal modelį. Reikšmės randamos kaip reikšmės funkcijos, kuri nustatoma ištyrus reiškinio dėsningumus.

Žinoma, kiekvienas iš šių metodų leidžia parinkti tik tikėtinas reikšmes. Kuo daugiau žinome apie reiškinio prigimtį, tuo geriau galime parinkti interpoliacijos ar ekstrapoliacijos metodą ir tiksliau įvertinti nežinomas reikšmes. Metodo patikimumas gali būti patikrintas, praktiškai išmatavus teoriškai apskaičiuotas reikšmes.

Svarbu yra tai, kaip pasiskirstę “žinomi” taškai, ypač jei jų nedaug (tada atsitiktinai parinkti taškai gali nebūti būdingi, pavyzdžiui, griovos dugnas, kalvos viršūnė lygumos reljefe). Blogiausia, kai tiriama erdvė nėra tolydi, t.y., egzistuoja trūkiai, barjerai ir kt. Dažnai žinomi taškai erdvėje yra pasiskirstę netolygiai. Yra skirtingi reprezentacinių imčių sudarymo metodai, kurie, kaip ir interpoliacijos ar ekstrapoliacijos procedūros, parenkami priklausomai nuo tiriamo reiškinio. Ypač sunku interpoliuoti geologiniuose tyrimuose, nes tikslių duomenų turima mažai. Todėl šioje srityje išvystytas matematinis modeliavimas.

Naujame taške reikšmę skaičiuoti galima pagal vienintelį artimiausią tašką, pagal visus “žinomus” taškus, arba kurį nors tarpinį tarp šių kraštutinių variantų.

Skaičiuojant pagal dalį taškų, reikia atsižvelgti į šiuos kriterijus:

1. Bendras taškų skaičius, skaičiavimams naudojamų taškų skaičius.

2. Atstumas nuo skaičiuojamo taško.

3. Kryptis nuo skaičiuojamo taško.

4. Skaičiavimų procedūra.

Iš tiesų, kai kurie taškai skaičiavimams yra svarbesni negu kiti, pavyzdžiui, Floridos pusiasalio reljefas neturi įtakos Kalifornijos reljefui (atstumo cenzas). Yra bendros taisyklės, padedančios įvertinti taškų svorius:

1. “Žinomų” taškų turi būti pakankamai daug ir jie turi kuo tolygiau dengti visą tiriamą sritį.

2. Erdvinė autokoreliacija: kuo mažesnis atstumas tarp taškų, tuo jie panašesni – taigi, tuo didesnį svorį turi turėti artimi taškai.

8. Fraktalai: būdas vaizduoti natūraliems objektams.

Tarkime, kad modeliuojami realūs objektai turi aiškiai apibrėžtas ribas (žemėlapio modelis). Objektai gali būti natūralūs arba sukurti žmogaus.

Fraktalų geometrija kur kas geriau, negu Euklido, leidžia pavaizduoti realias esybes, kurių kontūrai netaisyklingi, bet atsikartoja skirtinguose masteliuose ar objekto dalyse, pavyzdžiui, medis, upė. Jas būtų galima modeliuoti ir geometrinėmis figūromis: kūgiais, cilindrais ir kt., tačiau fraktalai leidžia tą padaryti greičiau ir gaunamas vaizdas yra panašesnis į tikrąjį.

Fraktalų geometriją sukūrė Mandelbrotas 1982 apibendrinęs 20 a. darbus šia tema. Angliškas žodis Fractal reiškia fragmentą, dalį. Fraktalų geometrijos esmė yra objektų fragmentacija ir panašumas į pačius save.

Nors natūralūs objektai dažnai būna grubūs ir nereguliarūs, juos dažnai sudaro pasikartojančios formos. Keičiant mastelį būdingos kontūrų savybės taip pat dažnai išlieka – tai yra “struktūros struktūrose”. Bet kuri fraktalo dalis yra tokia pat sudėtinga, kiek ir jis pats.

Kaip tai daroma.

Begaliniu procesu geometrinė forma skaidoma kaip parodyta pav. (d) atkarpos atveju ir kiekviena dalis koduojama skaitmenimis.

Mažiausi segmentai, kurių yra labai daug, vadinami Kantoro dulkėmis.

Tokios struktūros kūrimas paremtas 2 objektais:

1. Iniciatorius. Tai pradinė figūra, pavyzdžiui, linijos segmentas. Jei iniciatorius – trikampis, fon Kocho kreivė (e) imituos snaigę.

2. Repetitorius. Tai modelis, pagal kurį generuojama struktūra sakidant pradinę formą į elementus. Jei skaidoma į 3 dalis, n-tajame žingsnyje gauname 2ⁿ segmentų. O panašumo santykis yra 1/3.

Fraktalinės “kreivės” yra tolydžios, tačiau neturi nei liestinių, nei išvestinių. Jų forma priklauso nuo mastelio. Jei fraktalo parametrai nesikeičia, gaunami taisyklingi objektai.

Jei pabandysime apskaičiuoti fon Koch kreivės, gautos iš pradinio lygiakraščio trikampio (Koch snaigės) plotą ir perimetrą, gausime įdomų rezultatą.

Perimetras kiekviename žingsnyje pailgėja iš 1 tiesios kraštinės į 4, kurių ilgiai po 1/3, t.y. – ¾.

Plotas tuo tarpu artėja į 1.6 pradinio trikampio ploto! Taigi, nors kreivė begalinė, jos ribojamas plotas yra baigtinis. Tokios kreivės naudojamos modeliuoti kranto linijoms, miško kontūrams ir pan.

Stochastiniai fraktalai.

Ne visada norime modeliuoti taisyklingais objektais.

Dažnai reikia, kad jie atrodytų natūraliai, pavyzdžiui, kaip vienos rūšies medžiai, kurie yra labai panašūs, bet vis dėlto šiek tiek skiriasi.

Tam generuojant fraktalą įvedamas atsitiktinis parametras, kaip Brauno judėjimo modelyje: stochastinis judėjimas aprašomas maždaug taip:

y = ½ (y₁+y₂) + us₀2^-lh ; čia u – atsitiktinis dydis, s₀- Gauso pasiskirstymo parametras; l – rekursyvumo lygmuo; h – fraktalo parametras, išreiškiantis jo “grubumą”.

Formulė reiškia, kad įvedama nedidelė paklaida, kuri mažėja, didinant rekursinį gylį. Kaip gali būti generuojama tokia paklaida laužtei, parodyta paveiksle (f) – perstumiant išilgai koordinačių ašies arba naudojant statmeną bisektorių. Dažniausiai procedūra yra kur kas sudėtingesnė, pavyzdžiui, modeliuojant reljefą.

Kompleksinių skaičių erdvėje fraktalinės kreivės analogas yra Mandelbroto aibė (Benoit Mandelbrot, IBM, JAV). Jai būdinga apytikslė mastelio simetrija – dariniai kartojasi begalinėje mastelių aibėje, bet ne visai tiksliai atsikartodami.Rekursinis žingsnis nuo iniciatoriaus s yra

x = s + x².

Jei s yra kompleksinis skaičius, gausime plokštumos taškus. Mandelbroto aibė laikoma sudėtingiausiu žinomu matematiniu objektu. Ji tinka modeliuoti debesims, kalnams, kraštovaizdžiams fantastiniuose filmuose.

Erdvę užpildančios kreivės.

Saugant duomenis galima sutaupyti vietos, jei sumažinamas informacijos kiekis išlaikant visus reikalavimus, pavyzdžiui, jei įmanoma trimatį objektą saugoti kaip dvimatį. Paveiksle (e) parodyti vienmačių kelių (linijų) einančių per visus dvimatės erdvės taškus pavyzdžiai. Tai gali būti variantai, kaip numeruojami tam tikrą sritį apimančių topografinių žemėlapių lapai (viena koordinatė vietoje dviejų). Trimatėje erdvėje, padalintoje į taisyklingas gardeles, tą taip pat galima padaryti.

Įdomi problema yra, kaip turi atrodyti kreivės, kurios užpildo visą erdvę (nors ir begalinę). Euklido erdvėje tai neįmanoma, bet galima laikyti, kad taškas yra ne taškas, o kubiukas su nykstamai mažėjančia kraštine, tai padaroma.

Pareikalausime, kad:

1. Kreivė eitų per kiekvieną daugiamatės erdvės tašką (bijekcija).

2. Du taškai, kurie yra kaimynai erdvėje, būtų kaimynai ir kreivėje ir atvirkščiai.

3. Kreivė turi tikti bet kokiam masteliui ir likti stabili net ir labai didelėje (begalinėje) erdvėje.

Visų sąlygų patenkinti kol kas neįmanoma, bet panašių kreivių yra (pav., g). JAV surašymo biuras naudoja Peano kodus duomenų blokų adresavimui.

5 TEMA

Topologijos elementai

Dabar ryšius erdvėje panagrinėsime ne pagal absoliučias padėtis, o pagal formų santykius, atskleisdami jų erdvinę struktūrą. Geometrines detales paprasčiausiai ignoruosime, tokiu būdu topologiškai riestainis ir puodelis su ąsa bus vienodi kūnai.

9. Tinklai ir grafai

Erdvė gali būti įsivaizduojama kaip begalinė aibė taškų. Bet tiriant reiškinį dažnai pastebime, kad jis ne kiekviename tolydžios erdvės taške yra apibrėžtas. Pavyzdžiui, tiriant hidrografinius ar transporto tinklus, įvairių parametrų matavimų taškai parenkami ant tų tinklų – iš tiesų, nėra prasmės kalbėti apie srauto tankį arba sudėtį ten, kur to srauto nėra.

Formaliai apibrėšime izotropines sąlygas kaip erdvės savybių vienodumą visomis kryptimis. Anizotropinės sąlygos reiškia, kad savybės kinta priklausomai nuo krypties. 2D ar 3D tinklai – tai anizotropinės struktūros. Tinklai gali būti realūs (upės, keliai) arba virtualūs (oro susisiekimo linijos, vandenyno srovės). Tinklai naudojami kaip modeliai įvairiose mokslo ir planavimo srityse – juos sudaro transporto linijos, vamzdynai, ekosistemos ir t.t.

Tokių sistemų struktūrą patogu vaizduoti grafais.

Pavyzdžiui, įsivaizduokime Lietuvos teritorijos geležinkelių žemėlapį. Atmeskime informaciją apie geležinkelio linijų formą, kryptį, ilgį, palikdami tik struktūrinius komponentus: mazgus (stotis) ir jungtis tarp jų.

Tokio generalizavimo rezultatas – grafas – turi tik kelis pagrindinius elementus.

1. Linijų sankirtos ar galiniai taškai, vadinami viršūnėmis arba mazgais.

2. Linijos, vadinamos briaunomis.

3. Tarpusavyje nesusieti junginiai, vadinami subgrafais.

4. Plotai, apriboti linijų, kurie yra tarp briaunų arba jų išorėje, vadinami sritimis.

Apibrėžimas. Grafas – tai aibė G XxXxL, kur X – taškų plokštumoje aibė, o L – linijų aibė. Grafiškai tai geometrinė figūra, sudaryta iš taškų – viršūnių ir juos jungiančių linijų – grafo briaunų (lankų).

Geometriškai viršūnė – tai vienas taškas, kuris neturi nei dydžio, nei kitų matmenų.

Briauna – tai tiesi ar kreiva savęs nekertanti linija su galais dviejose viršūnėse, nebūtinai skirtingose. Jei nėra nesujungtų briaunų (t.y., nėra subgrafų), kiekviena briauna jungia 2 viršūnes ir skiria 2 sritis. Kiekviena viršūnė gali turėti bet kokį skaičių briaunų. Jei tik viena briauna – tokia viršūnė vadinama kabančia. Jei iš viršūnės išeina nelyginis skaičius briaunų, viršūnė vadinama lygine, kitaip – nelygine. Viršūnės gali būti įvairiai sujungtos tarpusavyje.

Jungumas – svarbiausia grafo savybė, nors pradžios bei galo buvimas, orientacija ir kiti parametrai neretai turi reikšmę.

Jungtys gali būti planarinės arba ne (tada briaunos projekcijoje gali kirstis nesudarydamos mazgo – sunkiau pavaizduoti). Neplanarinę situaciją turime transporto tinkle – keliai, tuneliai, viadukai, tiltai, požeminės perėjos. Trimatis kūnas – tai objektas, sudarytas iš tarpusavyje susijungiančių sričių.

Taigi, grafas aprašo tam tikrus erdvinius ryšius ir jį galima panaudoti atskleisti erdviniam panašumui, pavyzdžiui, tinklų. Du grafai yra izomorfiški, jei yra abipus vienareikšmis atvaizdis tarp jų briaunų ir viršūnių, t.y., jungumo ir lietimosi savybės sutampa, nors forma gali skirtis (pav., a).

Ciklas – tai kelias iš viršūnės į ją pačią. Atskira grafo rūšis yra medis – tai grafas be ciklų. Medžiais dažnai naudojamasi sprendžiant uždavinius, kai perrenkami variantai (pvz., “kryžiukai-nuliukai”). Hidrografinis tinklas taip pat dažniausiai yra be ciklų.

Grafas (ciklinis arba ne), kuriame nurodyta kiekvienos briaunos kryptis, vadinamas orientuotuoju. Tokie grafai dažnai naudojami praktikoje, pavyzdžiui, sudarant gatvių eismo schemas, vandentiekio tinklus ir pan. Jei leidžiamas tik vienpusis eismas, reikia orientuoti gatves taip, kad bet kurias sankryžas jungtų orientuota grandinė – kartais vienpusio orientavimo neužtenka. Prie orientuotų briaunų galime nurodyti kokias nors skaitines ryšio charakteristikas, pvz., vidutinį srauto tankį (pav., b). Taip modeliuojami tiekimo, tvarkaraščių ir įvairūs kitokie uždaviniai.

Tinklo konfigūracija atspindi skirtingas sąlygas – nuo paprastų struktūrų, kai visos viršūnės yra sujungtos su viena, iki visų įmanomų sujungimų. Paveiksle (c) parodytos kai kurios specifinės konfigūracijos.

Grafus galima koduoti matricomis.

Grafų savybės ir apėjimo uždavinys

Pirmasis grafo sąvoką įvedė L. Oileris 1736 m. spręsdamas Karaliaučiaus tiltų uždavinį (ar galima pereiti 7 tiltus po 1 kartą ir grįžti į tą pačią vietą). Kelias, einantis per visas grafo briaunas vienintelį kartą vadinamas Oilerio keliu. Ciklas per visas grafo briaunas (kai grįžtama į pradinį tašką), vadinamas Oilerio ciklu.

Spręsdamas uždavinį Oileris nustatė grafo savybes:

1. Grafo nelyginių viršūnių skaičius visada lyginis. Kiekvieno grafo viršūnių laipsnių suma yra lyginis skaičius.

2. Jei visos grafo viršūnės lyginės, tą grafą galima nubraižyti neatitraukiant pieštuko nuo popieriaus ir nekartojant linijų, be to, braižyti galima pradėti nuo bet kurios viršūnės ir baigti toje pačioje viršūnėje – t.y., egzistuoja daug Oilerio ciklų.

3. Grafą, kuris turi lygiai 2 nelygines viršūnes galima nubraižyti neatitraukiant pieštuko nuo popieriaus ir nekartojant linijų, jei pradedama vienoje nelyginėje viršūnėje, o baigiama antroje (egzistuoja Oilerio kelias).

4. Neatitraukiant pieštuko nuo popieriaus neįmanoma nubraižyti grafo, kuris turi daugiau negu 2 nelygines viršūnes (taigi, 7 tiltų uždavinys neišsprendžiamas).

Grafas, kurį galima nubraižyti neatitraukiant pieštuko nuo popieriaus, vadinamas unikursaliąja figūra. Tai, pavyzdžiui, optimalus maršrutas aplankant visas įžymias vietas (jei transportas visomis briaunomis vienodas), valant gatves ir pan.

Grafą galima oilerizuoti pridedant papildomas briaunas, atkartojančias jau esamas.

Grafas vadinamas pilnuoju, jei kiekvienos dvi jo viršūnės yra sujungtos briauna. Jei pilnasis grafas turi n viršūnių, tai jis turi n(n-1)/2 briaunų.

Grafas vadinamas jungiuoju, jei kiekviena jo viršūnė nėra izoliuota, t.y., egzistuoja kelias iš kiekvienos viršūnės į kitą. Kelio radimo uždavinys yra labai aktualus geografams.

Grafais nebūtinai vaizduojami geografiniai objektai. Pavyzdžiui, viršūnėmis galima pažymėti valstybes, o briaunomis – diplomatinių santykių tarp jų buvimą. Šiuo atveju briauna rodys simetrinį sąryšį tarp elementų. Tačiau dažnai vaizduojamas ryšys nėra simetrinis, pavyzdžiui norint parodyti,

kurios įmonės tiekia detales kitoms įmonėms.

Grafas skaido plokštumą į nesikertančias sritis. Jei grafo viršūnių yra V, briaunų B, tai grafas skaido plokštumą į B-V+2 sričių. (2 – jei išorė laikoma sritimi, 1 – jei ne). tas santykis yra pastovus.

10. Grafų modeliai

D Pavyzdys.

Duota gyvenvietės gatvių schema, Kiek mažiausiai autobusų reikia keleiviams pervežti, jei kiekviena gatve, jungiančia dvi gretimas sankryžas, gali kursuoti tik vienas autobusas?

Tai – savybės, susijusios su grafo jungumu. Jos leidžia atsakyti į tokius klausimus kaip: vidutinis oro linijų aptarnaujamų miestų pasiekimo greitis, kelionės kainos pasikeitimas pastačius tiltą per sąsiaurį, kiek yra alternatyvių maršrutų siekiant išvengti kamščių.

Apėjimo uždavinys.

Tai labai dažnai praktiškai sprendžiamų uždavinių klasė: kaip optimaliai pereiti visomis gatvėmis (paštininkui, šiukšliavežei, kelių žymėjimo mašinai ir t.t.)

Tarkime, turime stačiakampį gatvių tinklą (pav., c). Paštininko atveju užtenka vieną karta praeiti visomis gatvėmis. Grafas atrodys kaip parodyta paveiksle - tai nėra Oilerio grafas, todėl ir ciklas per visas briaunas neegzistuoja. Reikia papildyti grafą iki Oilerio grafo, tada ciklą rasti lengva taikant paprastą algoritmą: einama briauna, kuri, kol įmanoma, nėra tiltas, tada ta briauna išmetama.

Antras pavyzdys – šiukšliavežės maršrutas (važiuoti reikia visomis gatvėmis po 2 kartus – viena ir kita puse). Atitinkamas grafas parodytas paveiksle (d).

Niujorko miesto tvarkymo transporto maršrutams sudaryti naudojamasi būtent grafų modeliais, taip sutaupant apie 25 milijonus dolerių per metus.

Keliaujančio agento uždavinys.

Tai taip pat labai dažnai praktiškai aktualus uždavinys, modeliojamas svoriniu grafu . Kaip parodyta paveiksle (d) ant miestus jungiančių kelių pažymėtos kelionės sąnaudos. Agentas turi pradėti kelią mieste A, aplankyti visus kitus miestus po vieną kartą taip, kad kelionės sąnaudos būtų minimalios, ir grįžti į A. Iš principo taip pat sprendžiami yra siuntinių pristatymo, mikroschemų gamybos ir įvairūs kiti uždaviniai.

Matematiškai – tai grafo apėjimo per viršūnes uždavinys. Jei toks ciklas egzistuoja, jis yra skirtingas nuo Oilerio ciklo, vadinamas Hamiltono ciklu. Deja, nėra teoremos nustatyti, ar grafe egzistuoja Hamiltono ciklas.

Kartais gali padėti Dirako teorema:

Jei jungusis grafas turi ne mažiau kaip 3 viršūnes, ir kiekviena iš jų yra susieta su ne mažiau kaip puse likusių viršūnių, Hamiltono ciklas tokiame grafe egzistuoja.

Jei visos viršūnės tarpusavyje sujungtos – tai pilnasis grafas. Pilnasis grafas su n viršūnių turi P_n-1, t.y., (n-1)! Hamiltono ciklų, iš kurių pusė yra atvirkštiniai.

Natūralus sprendimo algoritmas pilnajame grafe – perrinkti visus galimus ciklus, sudedant briaunų svorius ir išrinkti mažiausią sumą. Tačiau tokio algoritmo sudėtingumas auga kaip (n-1)!/2. tai reiškia, kad atitinkamiems n reikės maždaug tiek galingo kompiuterio darbo laiko, kiek parodyta lentelėje (“kombinatorinis sprogimas”).

n	(n-1)!/2	Kompiuterio laikas (1 mln ciklų per sekundę)
5	12	<1 sek
6	60	<1 sek
10	181440	<1 sek
20	6*10¹⁶	2000 metų
100	5*10¹⁵⁵	apie 5*10¹⁴² metų

Kol kas nėra žinoma jokio efektyvaus šio uždavinio sprendimo algoritmo. Tačiau yra daug apytikrio sprendimo algoritmo, kai rastas “trumpiausias” kelias skiriasi nuo tikrojo tam tikru dydžiu (retai pasitaikančiu dideliu arba dažnai pasitaikančiu mažu – neaišku, kas geriau).

Artimiausio kaimyno algoritmas.

1. Iš A einama į sekančią viršūnę “pigiausiu” keliu.

2. Einama toliau į sekančią viršūnę “pigiausiu” keliu.

3. Iš paskutinės viršūnės grįžtama atgal į A.

Mūsų pavyzdžio atveju šis algoritmas duoda geriausią sprendimą.

Dar geresnį priartėjimą gausime pritaikę artimiausio kaimyno algoritmą visoms viršūnėms iš eilės ir išrinkę geriausią variantą. Bet tada gerokai išauga algoritmo sudėtingumas.

Pigiausios jungties algoritmas

1. Bet kur grafe pasirenkama pigiausia briauna.

2. Parenkama sekanti pigiausia briauna taip, kad nesusidarytų nepilnas ciklas ir 3 briaunos neišeitų iš vienos viršūnės.

3. Iš paskutinės viršūnės grįžtama atgal į A.

Abu šie algoritmai dažniausiai duoda neblogą rezultatą, bet kai kuriais atvejais jis gali būti ir pats blogiausias (pavyzdžiui, jei grįžtama į A labai brangiu keliu).

Minimalaus tinklo uždavinys.

Tai uždavinys, sprendžiamas, pavyzdžiui, tiesiant elektros perdavimo linijas. Visi duoti objektai turi būti sujungti taip, kad tarp jų visų egzistuotų kelias, o tinklo svoris būtų minimalus. Tai reiškia, kad grafe reikia rasti minimalų jungųjį pografį be ciklų. Priminsime, kad jungusis grafas be ciklų vadinamas medžiu, o n viršūnių medis turi n-1 briauną. Medį sudaro upių tinklas, kuris susiformuoja natūraliai, o tiesiant vamzdynus, telefono ar kitokius tinklus, reikia optimizuoti sprendimą.

Kiekvienas jungusis grafas turi bent vieną jungiantį medį, kuris vadinamas grafo karkasu.

Jei grafo briaunoms nurodyti svoriai, galima rasti minimalų jungiantį medį. Kaip jį rasti? Pasirodo, tai įmanoma visada ir yra algoritmas, garantuojantis sprendinio optimalumą.

Kruskalo algoritmas (Bell laboratorijos).

1. Rasti pigiausią kelią grafe.

2. Rasti sekantį pigiausią kelią tokį, kad nesusidarytų ciklas ir 3 briaunos neišeitų iš vienos viršūnės.

3. Tęsti, kol bus panaudotos visos viršūnės.

Trumpiausių tinklų uždaviniai

Tarkime, kad kelių iš viso nėra, o jų tiesimo kaina vienoda. Raskime trumpiausią kelią, jei galima kurti papildomus mazgus. Optimalus sprendinys yra toks, kuriame tinklas susijungia 120^o kampu – tai įrodyta.

Toks taškas vadinamas Šteinerio tašku. Jei Šteinerio taškas yra grafo viduje, tai per jį sudaromas trumpiausias tinklas. Jei Šteinerio taškas yra grafo išorėje (taip yra, kai kuris nors išorinės figūros kampas didesnis už 120^o), tada trumpiausias tinklas yra minimalus jungiantis medis.

Toričelio procedūra Šteinerio taškui rasti.

1. Pasirenkama ilgiausia trikampio ABC kraštinė.

2. Sudaromas lygiakraštis trikampis BCX

3. Aplink jį apibrėžiamas apskritimas.

4. A ir X sujungiami atkarpa. Šteinerio taškas yra apskritimo ir atkarpos AX sankirtos taškas.

Kiekviename trumpiausiame tinkle vidiniai mazgai gali būti tik Šteinerio taškai.

Labirinto uždavinys.

Tarkime, kad turime figūrą, apribotą savęs nekertančia uždara linija. Nesunku pastebėti, kad, jei iš taško, esančio figūros viduje nubrėšime spindulį, tai bet kokio spindulio ir figūros kontūro sankirtos taškų skaičius bus lyginis. Galima suformuluoti savybę:

Jei lanko AB ir nesavikirtės uždarosios kreivės l sankirtos raškų skaičius nelyginis, tai vienas iš taškų yra kreivės l apribotos figūros išorėje, o kitas – viduje. Kitaip abu taškai A ir B yra arba figūros viduje, arba jos išorėje.

Šios savybės naudojamos GIS sistemose erdvinei duomenų analizei.

“Labirinto” taisyklė. Įeinant į labirintą ir apeinant visus jo vingius ta pačia ranka reikia liesti sieną tol, kol išeinama iš labirinto.

Žemėlapio spalvinimo uždavinys.

Naudojant minimalų skaičių skirtingų spalvų nuspalvinti politinį žemėlapį. Tai nėra taip jau paprasta. Šis uždavinys domino daugelį matematikų ir 1879 A. Kelis (Anglija) paskelbė hipotezę, kad bet kokį politinį žemėlapį galima nuspalvinti keturiomis spalvomis taip, kad kaimyninės valstybės būtų skirtingų spalvų. Tačiau atrodo, kad iki šiol hipotezės nepavyko nei patvirtinti, nei paneigti.

Žemėlapį galima laikyti grafu. Yra įrodyta su tuo susijusių dalykų.

1. Bet koks žemėlapis plokštumoje turi bent vieną sritį, kurios briaunų skaičius mažesnis kaip 6.

2. (Dviejų spalvų teorema). Būtina ir pakankama sąlyga, kad žemėlapį būtų galima nuspalvinti 2 spalvomis – iš tą žemėlapį vaizduojančio grafo kiekvienos viršūnės turi išeiti lyginis skaičius briaunų (valstybių sienų).

3. (Trijų spalvų teorema). Būtina ir pakankama sąlyga, kad žemėlapį būtų galima nuspalvinti 3 spalvomis – tą žemėlapį vaizduojančio grafo kiekviena sritis privalo turėti lyginį skaičių briaunų.

4. (Penkių spalvų teorema). Bet kokį žemėlapį, kurio visų viršūnių laipsniai 3 (normalusis žemėlapis; jis lengvai gaunamas didesnio laipsnio viršūnes pakeitus apskritimais), galima nuspalvinti 5 spalvomis.

11. Geografinės informacijos geometrija

Topologiniai žemėlapiai – tai žemėlapiai, kuriuose iškraipomos formos, bet išsaugomos topologinės savybės: persidengimas, kaimynystė, “skylės”. Žemėlapyje grafo viršūnės dažniausiai turi 3 briaunas (nors gali būti 2, 4 ar daugiau). DLG (Digital Line Graph) – tai JAV Geologijos tarnybos naudojamas modelis topografinei informacijai koduoti. Jam apibrėžti topologinio vientisumo reikalavimai (mozaikos struktūrai):

1. Kiekvienas vienmatis objektas (briauna) jungia 2 nulinio matavimo objektus (viršūnes).

2. Kiekvienas vienmatis objektas (briauna) skiria 2 dviejų matavimų objektus (sritis).

3. Kiekvienas nulinio matavimo objektas yra apsuptas briaunų ir sričių ciklo.

4. Kiekvienas dviejų matavimų objektas yra apsuptas briaunų ir viršūnių ciklo.

5. Nėra sankirtų, kitokių nei viršūnės.

Ignoruojami izoliuoti objektai, taigi topologiniai taškai atskiriami nuo pavienių taškų.

Ne visi kartografiniai objektai yra topologiniai, pavyzdžiui, forma, kreivumas ir kt. Keli skirtingi žemėlapiai gali turėti vienodą topologinę struktūrą. Topologinė struktūra yra invariantas transformacijų atžvilgiu (perstūmimo, tempimo bet ne plėšymo): keičiant atstumus ir kampus, 4 dalykai turi likti pastovūs:

1. Briaunų ir viršūnių susietumas.

2. Sankirtos.

3. Kaimynystė.

4. Įdėtumas.

Iš linijų topologinę struktūrą sukurti nėra paprasta, bat patogu, nes grafų savybėmis neretai pasinaudojama digitavimo klaidoms aptikti. Būdingiausios digitavimo klaidos yra tokios.

1. Yra nesujungtų briaunų.

2. Poligonas neuždaras.

3. Yra dvigubų briaunų ar viršūnių.

4. Yra daugiau nei 1 arba nė vieno centroido.

5. Viršūnė turi ne lygiai 3 briaunas (tai – nebūtinai klaida).

6. Trūksta poligono.

7. Yra nereikalinga sankirta.

8. Yra netyčinis mazgas.

9. Netaisyklinga linijos forma.

Klaidos automatiškai dažniausiai aptinkamos naudojant Oilerio lygybę.

Operacijos su geografiniais duomenimis.

Linijų sankirta

Jei turime dvi atkarpas AB ir CD, kur taškų koordinatės yra A(x1, y1), B(x2, y2), C(x3, y3), D(x4, y4), jų sankirta yra atitinkamų tiesių y = ax+b ir y=cx+d sankirta, t.y., ax+b =cx+d, kur koeficientai a, b, c ir d apskaičiuojami įsistačius žinomus taškus A, B, C ir D į tiesių lygtis.

Taško buvimas poligone.

Dažnai reikia nustatyti, ar taškas patenka į daugiakampio vidų. Tam naudojama Žordano teorema, atitinkanti labirinto taisyklę grafe:

Nuo taško viena kryptimi brėžiamas spindulys taip, kad jis nusitęstų už poligono ribų.

Tada skaičiuojamos spindulio sankirtos su poligono briaunomis.

Jei sankirtų skaičius yra lyginis, taškas yra poligono išorėje, jei nelyginis – viduje.

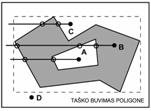
Kad būtų paprasčiau, naudojami koordinačių ašims lygiagretūs spinduliai. Žinoma, prieš tai pirmiausia patikrinama, ar taškas patenka į poligoną apimantį stačiakampį (jie ne, jis, žinoma, yra išorėje).Panašiai tikrinama, ar taškas yr aant linijos, ar linija kerta poligoną ir kt.

Taško buvimas viename iš daugelio poligonų.

Galima tikrinti visus taškus iš eilės (sudėtingumas - n), galima poligonus sutvarkyti hierarchiškai (sudėtingumas – log₄n).

Centroido skaičiavimas.

Centroidai naudojami, kai reikia pažymėti poligono (arba linijos) vienintelį “centrinį” tašką.

1. Pagal viršūnes.

x_c =(1/n) S x_i; y_c =(1/n) S y_i). Jeigu poligonas labai netaisyklingas ar turi vienoje pusėje neproporcingai daug viršūnių, rezultatas nebus geras.

2. “Svorio” centras apskaičiuojamas statistiškai.

3. Apimančio ar įbrėžto stačiakampio, skritulio ar kitos taisyklingos figūros svorio centras.

4. Aukščiausia poligone esanti viršūnė ar kitoks reprezentuojantis taškas.

5. Intuityviai pažymėtas.

Atstumų, plotų, kompaktiškumo įvertinimas.

Atstumai dažniausiai randami pagal Pitagoro teoremą. Plotai skaičiuojami pagal formulę

Formos sudėtingumą nusako:

a) poligono perimetro santykis su to paties ploto skritulio perimetru,

b) spindulių iš centroido nuokrypių nuo apskritimo spindulio suma (tam reikia gerai parinkto centroido).

Poligonų persidengimas ir sąjunga.

Norint rasti persidengimą ar sąjungą, poligonai skaidomi į trapezoidus.

Poligonų struktūros (mozaikos ir gardelės)

Erdvę galima diskretizuoti įvairiai. Diskretizavimas – tai tolydžios erdvės skaidymas į segmentus, t.y., į poligonus.

Mozaikos – tai besiliečiančios zonos, kurios dengia visą erdvę. Jos gali būti taisyklingos (geometrinės figūros, topografinio žemėlapio lapai) ir netaisyklingos (sklypai, žemėlapio objektai).

Nereguliarios mozaikos tai (begalinis) skirtingos formos ir dydžio poligonų junginys (3D - poliedrų). Tai dažniausiai socialinių, ekonominių, demografinių duomenų zonos, sklypai, trianguliaciniai paviršiaus modeliai.

Nereguliarios mozaikos tai pasikartojančių vienodų taisyklingų geometrinių figūrų junginiai. Tai tinklelio kvadratai, diskretizuojant gauti vaizdai, tolydžių imčių duomenys. Taisyklingas struktūras daug lengviau analizuoti ir apdoroti.

Gardelės – tai taškų struktūros, pakeičiančios poligonus. Jos gali būti sankirtos arba centroidų taškai.

Keičiant mastelį, taisyklingos struktūros generalizuojamos pagal “piramidės” modelį (pav.).

Netaisyklingos struktūros koduojamos ir generalizuojamos kitaip (paveiksle parodytas Quadtree modelis).

Nereguliarios mozaikos dažnai naudojamos Tiesen’o (Voronoi) poligonams sudaryti. Jie sukuriami sujungus centroidus ir padalinus gautas linijas statmenais bisektoriais, bei surinkus poligonus iš susidariusių briaunų. Matematikoje toks poligonas vadinamas Dirichlė sritimi.